Cyber risk matrices are ubiquitous in the cyber security world. They are simple to understand but mask and confound the thing they seek to communicate.
The cyber risk matrix forces flawed risk conclusions. Evidence shows the results are not only a flawed understanding of risk, but a decision-making and prioritization process that is so poor, assigning possible decisions to rolled dice would produce better outcomes.
For risks with negatively correlated frequencies and severities, they can be “worse than useless,” leading to worse-than-random decision
L. A. Cox Jr, MIT trained risk expert, “What’s wrong with Risk Matrices?”, Abstract
The cyber risk matrix is a visual medium to describe different levels of risk, it is not itself risk analysis process. However, the plotting of analytic conclusions within the structure of the matrix ensures meaningful risk analysis results remain hidden behind a fog of unearned confidence.
What’s Wrong with the Cyber Risk Matrix?
Cyber risk matrices are incapable of answering the one question they were meant to answer: What is the risk of loss in the event of a cyber event? High, medium, or low is not the answer to that question. Even worse, the matrix creates risk with a bit of dramatic irony.
Risk is a function of uncertainty. That is risk depends on uncertainty. No uncertainty, no risk. If there is a certainty action X will, in fact, result in Y, and Y is undesirable, then don’t do X. If action X may result in Y but it could also result in Z or Q, the uncertainty of outcome exists. If Z, Q, or any other number of potential outcomes are bad not only does risk exist, but now risk analysis comes into play.
Any risk-analysis methodology needs to answer the question of loss otherwise it has no good reason to exist. The collective desire to measure risk comes down to measuring the potential cost of the loss of life, limb, or money (in no particular order) and then prioritizing controls to reduce those risks. We care about car accidents because they hurt people and we have to spend money to get another car, not because car accidents are inconvenient.
If risk was only measured to gain a better understanding of the severity of the feeling of inconvenience when our houses burned down, or our cars got plowed into, or a mudslide took out the nearby power plant, then we could “eliminate” all the risk with a sufficient dose of Soma.
We measure risk to decide which controls are worth receiving limited funds.
Cyber risk matrices, and their underlying risk analysis methodology, don’t help the interpreter decide which controls are worth spending money on, any more than throwing bones informs a decision to go skydiving tomorrow.
There are two fundamental aspects (features, not bugs) of the matrix at the root of this problem: ordinal scales and severity ranking. Used properly, ordinal scales and severity rankings are not bad, but the way they are baked into the cyber risk matrix cake generates unavoidable mistakes. Trying to avoid them, or work around them are not viable solutions. Both features are irrevocably tied to the analytical and “visual” units of likelihood and impact. To actually avoid them is to trash the matrix altogether.

1. Ordinal Scales Misuse
Ordinal scales are hidden behind the color-coded severity (low – critical) of the above image. Often the scale is a range from 1-5 or 1-10 and sections of the range are mapped to likelihood, impact, and severity. For example, a 10-point severity scale could have this mapping: Low is 1-3, Medium is 4-6, High is 7-9, and Critical is 10. There are also similar financial impact-scale mappings – Low is < $50k, Medium is $50k – $300k, etc.
There are only 4 scales of measurement and only one of them (ratio) is useful for probability and financial math; the ordinal scale does not allow for probability or financial math. Ordinal scales are fine for ranking but there is no way of “knowing the difference” in any mathematically meaningful way.
Food and metal hardness scores are examples of the ordinal scale for measurement. Imagine trying to combine two 2-star meals to produce a single 4-star meal and the problems with ordinal scales behind the risk matrix begin to emerge.
Are two 5-rated Mediums equal to a single 10-rated Critical?
Ordinal scales in the risk matrix force, what L. A. Cox Jr. calls, “range compression”:
Discrete categorization lumps together very dissimilar risks, such as an adverse consequence of severity 0 occurring with probability 1 and an adverse consequence of severity 0.39 occurring with probability 1.
Cox, What’s wrong with Risk Matrices, pg. 506
In How to Measure Anything in Cyber Security Risk, Richard Serrision calls this phenomenon “extreme rounding”:
Range compression is an … extreme rounding error introduced by how continuous values like probability and impact are reduced to a single ordinal value.
How to Measure Anything in Cyber Security Risk
The matrix masks this compression, and it can get so severe two different risks end up “compressed” together into the same cell, especially on the upper and lower bounds. Opposing severity risks can even end up in cells that would indicate the opposite is true.
2. Severity Ranking Ambiguity
Severity is an ambiguous ranking term that is the product of likelihood and impact. An example derived from the above matrix:
Critical severity = High impact + High likelihoodThe ambiguity of severity emerges from the wide range of possible interpretations of likelihood and impact. There are multiple studies regarding vast spectrum of interpretation even when strict definitions (i.e. ranges) where assigned to the terms.
The results were impressive. Even with defined probability ranges (ex. likely is 66%-90%), 43% – 67% of the participants would still plot statements similar to “It is likely that a data breach resulting in heavy losses will occur in the next year” outside of that strict range.
These results suggest that the method used by the IPCC is likely to convey levels of imprecision that are too high.
Budescu DV, Broomell S, Por HH. Improving communication of uncertainty in the reports of the intergovernmental panel on climate change. Psychol Sci. 2009 Mar;20(3):299-308. doi: 10.1111/j.1467-9280.2009.02284.x. Epub 2009 Jan 30. PMID: 19207697. Emphasis mine.
Attempts to define impact within strict buckets (ex. $0 – $100k is low impact) do not fare any better. Participants still bring ideas to the statements “allowing” them to alter its interpretation resulting in a wide range of plotting possibilities on the matrix.
To make matters worse, there is no consistency across bucket ranges (1-5 vs 1-10) even when low and high are defined as the exact same bucket.
It turns out even with all things being equal, severity plotting on the cyber risk matrix is neither a reliable nor repeatable process. That is if 100 participants were given the same information along with the same strict likelihood and impact ranges, the severity plot points would end up all over the map.
Why is the Cyber Risk Matrix Considered Important?
In general, the risk matrix is important because it’s easy to read and has been around a long time, not because it works. That may seem like a silly reason for a thing to be important, but the risk matrix has been around so long it has entered into risk management canon. As it grew in acceptance, mostly because it was easy to implement, explain, and read, it grew in “authority”. Until one day it gained “IBM Prestige” and not using the risk matrix earned funny looks.
No one ever got fired for choosing IBM
Unknown, but axiomatic
With the now ubiquitous use, and historical prestige, the quote is applied to the risk matrix:
No one ever got fired for using a risk matrix
Cloak & Cyber. Just now, we think
In total, the risk matrix is important because … it’s important. It’s not important because its conclusions help organizations better understand and reduce risk.
What are the Limitations of Using a Cyber Risk Matrix?
A primary limitation of the cyber risk matrix is the lack of capability to present the value of risk-mitigating controls in any meaningful way.
If expected loss (EL) exceeds an organization’s ability to withstand that loss, action must be taken. In general, those “actions” are the spending of funds on risk-mitigating controls: insurance, technology, process improvement, etc.
Plotting severity on the matrix does not inform that decision in any way. It’s superfluous to the entire process. The matrix is not needed to describe a “greater than” condition. The act of plotting the severities on the matrix (issues described in the What’s Wrong with the Cyber Risk Matrix? above) often leads to the miss prioritization of activities.
Either an EL of $1.4 million exceeds the bankruptcy threshold of $10 million or it does not. And if the EL exceeds a certain risk tolerance threshold, how much is it worth spending on the controls? The matrix cannot provide this control value information.
Should I Use the Cyber Risk Matrix?
No one should use the cyber risk matrix, not if the choice exists anyway. No one should use it any more than anyone should have gone to Galen for one of his mighty elixirs of life or made medical decisions based on the Miasma theory on diseases. The situation though is understandable. Paradigm shifts at this level are tectonic. When dealing with an idea or practice this widespread and rooted in academia, government, and the private sector we are dealing with jobs, careers, tenures, reputations, etc.
This won’t change overnight.
So, if you have to use the matrix here is one way to use it that is less terrible: How to Use the Risk Matrix
What is a Cyber Risk Matrix Alternative?
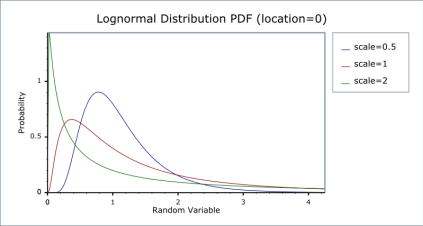
Probability distribution graphs are better at providing meaningful visual detail than the risk matrix. They can accomplish the visualization goals of the matrix without the underlying issues described above. Each graph has its own strengths and weaknesses, but each graph is an improvement over the risk matrix.
Some example distribution graphs are:
Logarithmic distribution
Normal Distribution

Binary (Bernoulli) Distribution

Uniform Distribution

The Cyber Risk Matrix in the Final Analysis
The (cyber) risk matrix is worthless and still around for one reason: easy readism*. Easy readism (a term I’m certain I just coined) is the decision to prioritize readability over reliability with the effect of grossly oversimplifying the results of a process to such an extent that acting on the results is as likely to bring harm as it is to bring good.